Get in Loser, We're (Almost) Going to Neptune

If you know where you're going, when you want to leave, when you want to get there, and any stops you need to make along the way, you can calculate how much delta-V is required for a space journey. Based on my mission concept outline, I knew all of that at a high level:

• Starting Point: Earth
• Stops Along the Way: Jupiter for a gravity assist
• Ending Point: Neptune's L5 Lagrange Point
• Departure Time: sometime between 2040-2060
• Arrival Time: sometime between 2040-2060 + transit time

What follows is my back of the napkin math to get to a delta-V estimate. If you're not a fan of math, you can just skip to the "answer" at the end of the post.

The Basics

Delta-V

The goal of this exercise is to arrive at an estimate of delta-velocity for an outbound mission to Neptune's L5 Lagrange Point. That is, the change in velocity (measured in kilometers per second or km/s) required to start at one place and end at another. These numbers are always positive regardless of whether the spacecraft is accelerating or braking relative to the nearest body of interest.

Launch Windows

A launch window is a range of time when there are good conditions for traveling from one planetary body to another. This is when the planets are aligned just right to support a long journey. Launch windows are only important to consider in a technologically constrained story when there are limitations on fuel or thruster power. 

Orbital Elements

Orbital elements are a way of defining the characteristics of an object's orbit around the sun. It is possible to propagate the orbit of an object so that its rough location is known at any given date. I say "rough" because the easy solutions to orbital elements exclude the effect of perturbations which can have small but very significant effects for planning far into the future. 

Anyway, the orbital elements for all of the planets in the solar system are well understood. Since my final destination is not Neptune proper but rather its L5 Lagrange Point, I started with Neptune's position and subtracted 60 degrees from the Mean Anomaly variable. The Mean Anomaly is a measurement of the planet's position in orbit around the sun, and L5 Lagrange Points trail 60 degrees behind each planet (further reading here). So, if you kind of squint at the logic, this makes enough sense for estimation purposes.

Porkchop Plots

Porkchop plots are a tool for estimating the required delta-V to move from one planetary body to another. The math underlying the plots makes a lot of simplifying assumptions. It's a great tool for estimating the feasibility of a mission but it does ignore important and potentially substantial contributors to a mission trajectory, like the N-body problem and effect of solar radiation pressure. 

A porkchop plot will tell us the following for a given range of time, starting body, and ending body:

• How much delta-V is required for an object in the starting body's orbit (IE the same orbit as Earth takes around the sun) to enter an orbit around the sun that intersects the ending body's orbit
• How much delta-V is required to leave orbit of the sun and enter the ending body's orbit (IE the same orbit as Jupiter takes around the sun)
• The effect of varying departure date and time of flight on delta-V

I used the EasyPorkchop tool for all the plots in this post. Here's an example, that I'll use again below, and how to read it.

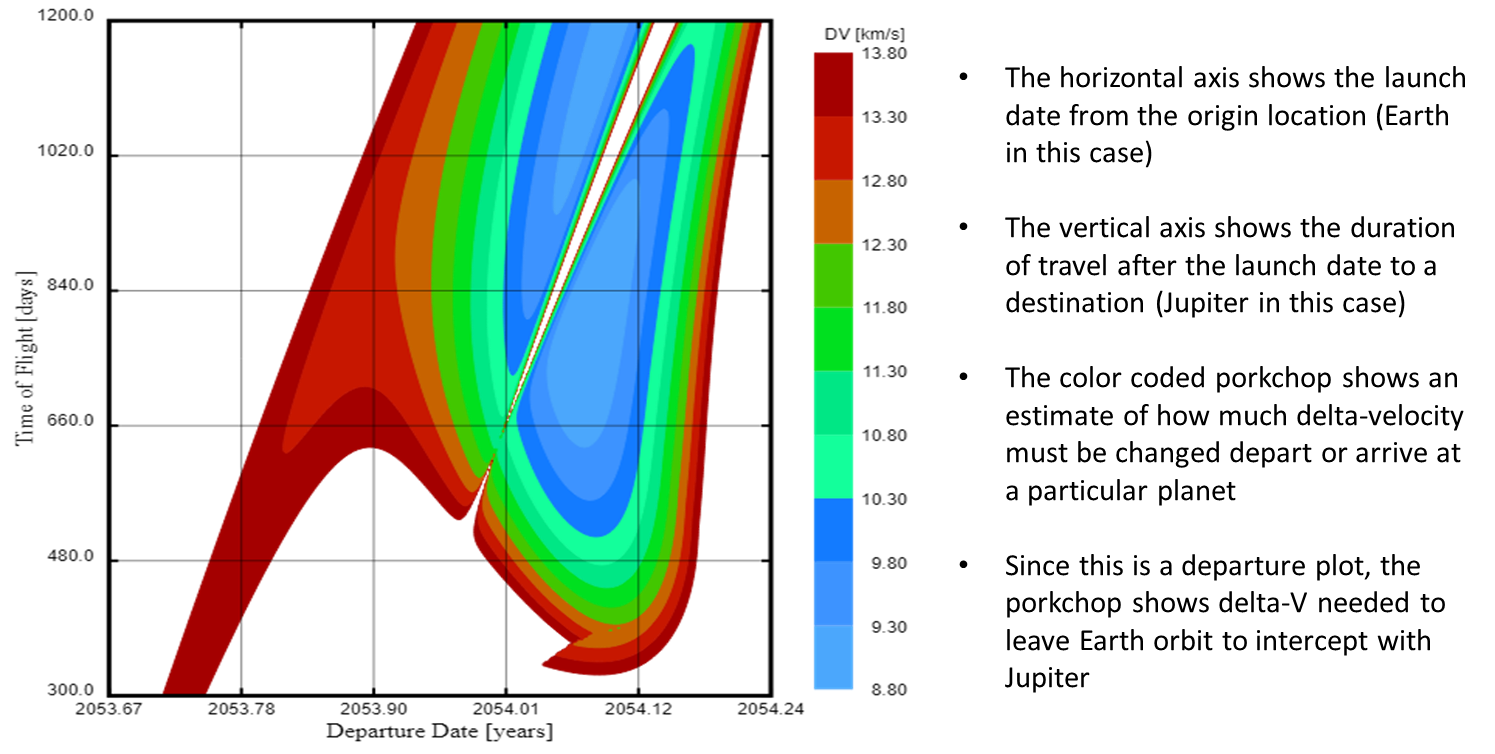
Launch Window Refinement

Because I made my own life harder and split Aspire's trajectory into two distinct segments, I need to consider launch windows from the perspective of Earth to Jupiter, then Jupiter to Neptune's L5 Lagrange point. Viewing Earth-Jupiter and Jupiter-Neptune L5 departure porkchop plots for 2040-2060 gives us the following:

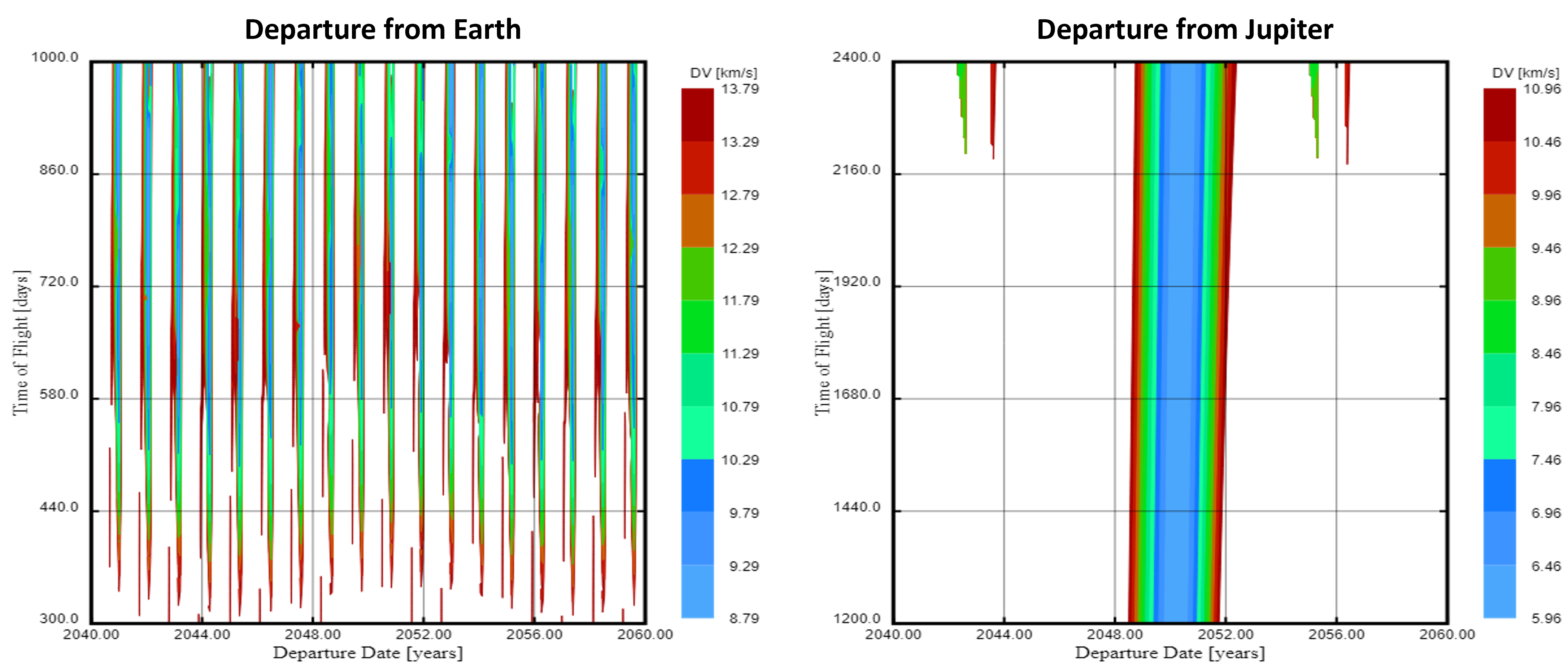
These results make a lot of sense when you consider the orbits of the planets involved. Earth makes a full rotation around the sun once a year, so, intuitively, there will be a good launch opportunity for a trip to Jupiter at least once per year. Similarly, Jupiter makes a full trip around the sun once every 13 years, so a Jupiter-Neptune L5 trip has very limited options, with one ideal launch window and several less ideal "sliver" shaped launch windows.

Looking a little deeper at the results, it is interesting to note that the ideal Jupiter-Neptune L5 launch window in 2048-2052 coincides with less ideal Earth-Jupiter launch windows, which you can eyeball on the left chart by the minimum time of flight being a bit longer and more red/less blue in that range.

Anyway, we've basically got two options: the ideal window at Jupiter and the less ideal "sliver" window. I'm actually going to use the less ideal option, though the final delta-V numbers between the two alternatives end up being pretty close.

Earth-Jupiter Segment

Here are the porkchops for a much narrower range of time. The plot on the left is the departure from Earth; the plot on the right is the arrival at Jupiter.

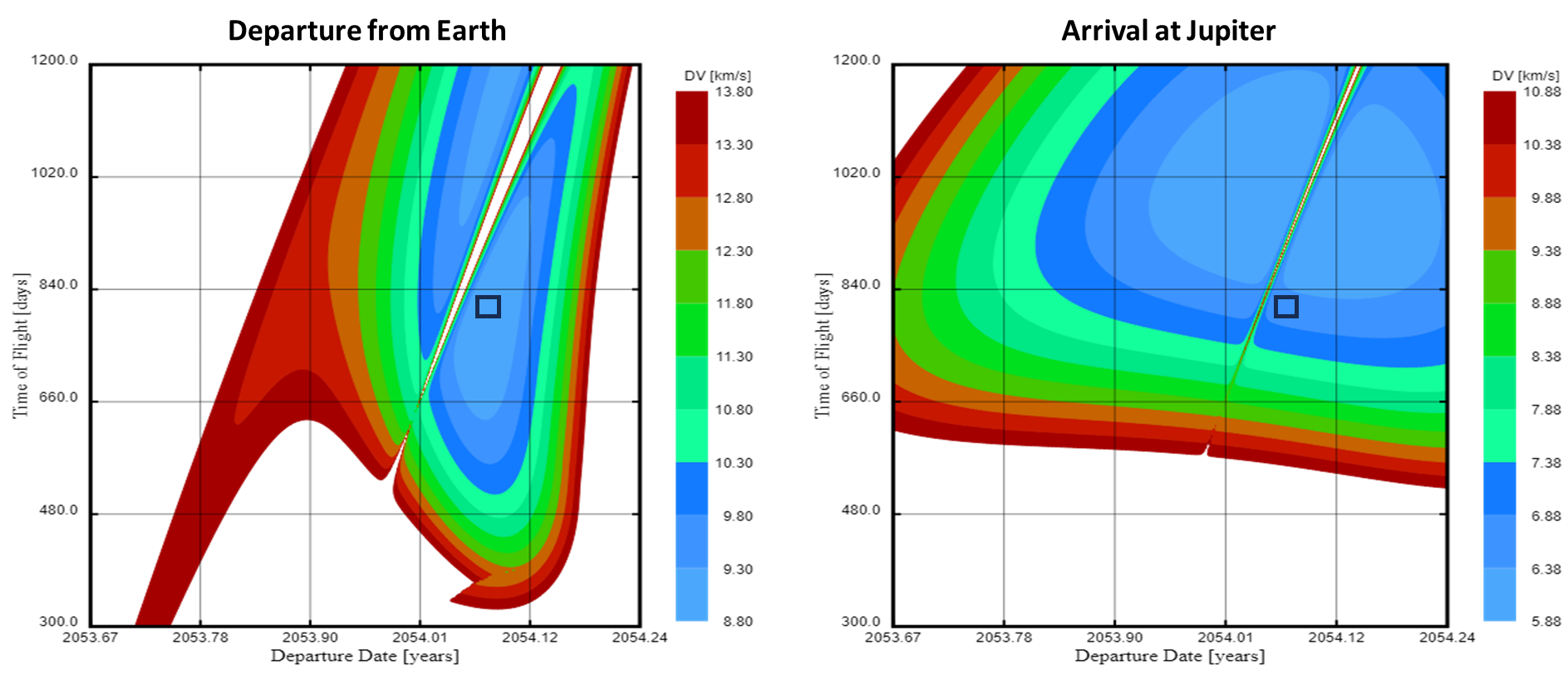
I've added a square on each plot to show the desired launch date, flight time, and delta-V. Keep in mind that this is not the most optimal arrival date for Jupiter as shown by the darker blue delta-V. Using these plots, here's what we have so far:

• Earth Departure Date: 1/22/2054
• Earth Departure Delta-V required: 8.8 km/s
• Transit Time: 800 days
• Jupiter Arrival Date: 4/1/2056
• Jupiter Arrival Delta-V required*: 6.5 km/s

*More on this in a bit

Jupiter-Neptune L5 Segment

Here are the porkchops for the next segment of the journey. Jupiter departure is on the left, Neptune-L5 arrival on the right. These plots are focused around the 4/1/2056 Jupiter arrival date.

The plot on the left shows a close up of one of the "sliver" launch windows. This is why the Jupiter arrival selection was a little less than ideal--I needed to hit this pretty narrow window of opportunity to get to Neptune's L5. Using these plots, here's what we have for this leg of the journey:

• Jupiter Departure Date: 4/1/2056
• Jupiter Departure Delta-V required*: 10.3 km/s
• Transit Time: 2280 days
• Neptune-L5 Arrival Date: 6/29/2062
• Neptune-L5 Arrival Delta-V required: 11.5 km/s

*More on this next

Making Sense of a Jupiter Transit

Here's where my math and logic will get the most hand-wavy. I want Aspire to use Jupiter for a gravity assist. Instead, the porkchop plots have given us numbers for...

• At Jupiter arrival, the delta-V required to rendezvous (6.5 km/s) - generally this is a reduction in velocity relative to the sun
• At Jupiter departure, the delta-V required to intersect Neptune's orbit (10.3 km/s) - generally this is an increase in velocity relative to the sun

My logical leap here is that in order to estimate the delta-V required at Jupiter, what I really want is the absolute value of the difference between these numbers. I think that will represent the magnitude of additional delta-V needed to alter the trajectory to reach Neptune. I can't answer how much delta-V the Jupiter gravity assist is providing without an extra level of math and some additional tools (and re-learning some things I've forgotten since college). So, I know it provides some benefit that I'm unable to account for.

As a result of this handwavy logic, I contend that the Aspire must provide an additional 3.8 km/s of delta-V at Jupiter to get to Neptune.

Tying it all Together

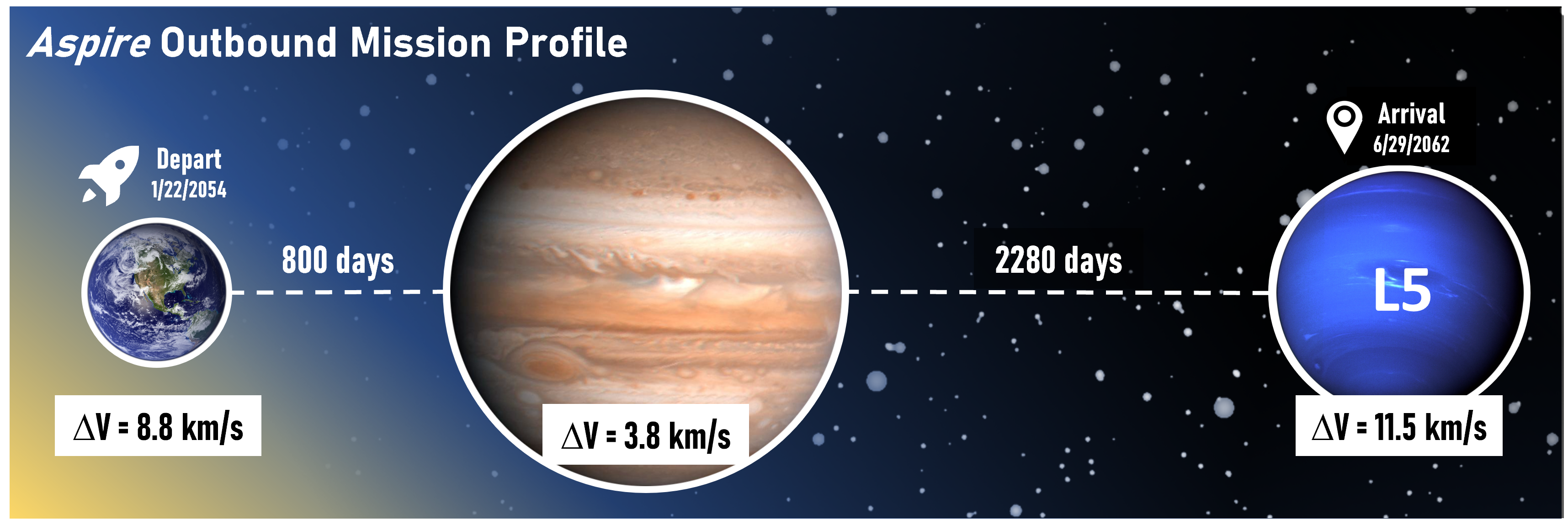
First, a moment of silence for my lackluster graphics design talent.

Now, the final answer:

• Earth Departure: 1/22/2054
• Neptune L5 Arrival: 6/29/2062
• Total Outbound Delta-V: 8.8 + 3.8 + 11.5 = 24.1 km/s

Of course, it seems reasonable that many of the astronauts might want to return home at the end of the mission. So, rather than attempting to porkchop my way back to Earth, I'll just double that delta-V budget to ~50 km/s. 

Now that we have a full mission delta-V budget, the next step is to size an engine and power plant capable of supplying that. Thank goodness this is a near-future story with a couple technological leaps, because that is a lot of delta-V.